Soluciones lección 033 a 035
Página 1 de 1.
 Soluciones lección 033 a 035
Soluciones lección 033 a 035
Soluciones en pseudocódigo correspondientes a ejercicios seleccionados de los propuestos para las lecciones 33, 34 y 35:
No pondré los códigos en Modula acerca de las soluciones seleccionadas, sino que les daré un pseudocódigo a modo explicativo de cómo debería funcionar la solución, de este modo ustedes tendrán más o menos un camino a seguir y volver a intentar. Esto contribuirá a que tengan que pensar mucho para lograr aplicar la recursividad y así logren comprenderla de verdad. Obviamente yo estaré disponible para cualquier consulta que tengan ya que algunos ejercicios son muy complicados.
====================================================================================
Ejercicio 1:
Si ambas listas son vacías las listas son iguales y se devuelve true.
Si cualquiera de las listas es vacía, las listas son distintas y se devuelve false, de lo contrario, se obtiene el primer elemento de cada lista y se comparan. Si ambos elementos son iguales se llama recursivamente a la función con el resto de cada una de las listas.
Si los elementos del comienzo de cada una de las listas son diferentes, las listas también son distintas (en por lo menos un elemento), por lo que se devuelve false y las llamadas recursivas terminan.
-------------------------------------------------------------------------------------
Ejercicio 10:
La primera dificultad del ejercicio consiste en decidir sobre qué tipo inductivo se va a definir la función. Resulta claro que el resultado de la función es un natural. Por lo tanto tendríamos:
CaminosPosibles → Retorna un CARDINAL.
Además podría pensarse que la función es sobre una lista (vinculada a los adoquines) y un número natural (que indica el adoquín objetivo). Esto nos daría:
CaminosPosibles: LNat → CARDINAL
Esta notación indica que la función recibe algo de tipo LNat y retorna algo del tipo CARDINAL, tal como la notación matemática para funciones. Es decir
NombreDeLaFunción: Dominio (es decir lo que recibe) → Codominio (es decir, lo que retorna).
De todas formas tratemos de resolver el problema con menos información , esto es, solo con el natural que indique el adoquín objetivo. Entonces definimos nuestra función así:
CaminosPosibles: CARDINAL → CARDINAL
es decir, recibe un CARDINAL y devuelve un CARDINAL.
Exploremos si con esta definición se puede realizar lo pedido. Además como primera aproximación hagamos una tabla que tenga el largo de la lista y la cantidad de caminos posibles. La cantidad de caminos posibles se halla mediante una búsqueda exhaustiva.

Teniendo en cuenta las condiciones:
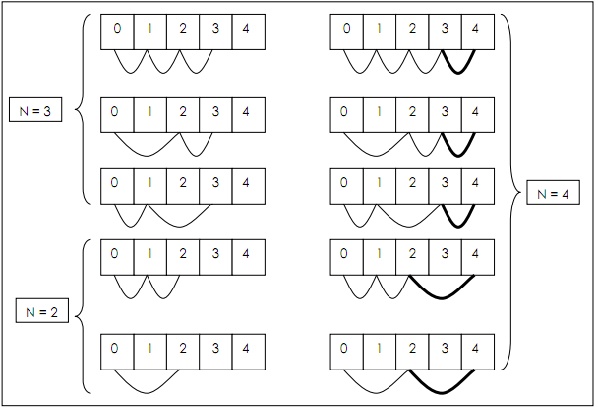
Supongamos que queremos calcular la cantidad de caminos para N = 4. En la Figura se ven los caminos posibles para N = 3 y para N = 2, luego por la condición 1 se hace un salto de un adoquín para obtener algunos de los caminos para N = 4, partiendo de los caminos de N = 3. El resto de los caminos se obtienen tomando los caminos para N = 2 y aplicando la condición 2, saltando 2 adoquines. Como estos son todos los caminos posibles, podemos pasar a formalizar:
Ejercicio 12: Problema de las Torres de Hanoi
El problema de las Torres de Hanoi es un puzzle matemático o juego inventado en 1831. Dicho juego consta de N discos, todos de tamaños diferentes, y 3 sitios, A, B y C (también llamados cilindros) en donde se pueden apilar los discos. En el estado inicial los N discos se encuentran apilados de menor a mayor en el cilindro A, formando una torre tal como se indica en la Figura 1.

En el estado final los N discos se encuentran apilados de menor a mayor en el cilindro C, formando una torre tal como se indica en la Figura 2.

Para alcanzar este objetivo debemos tener en cuenta dos reglas:
Una solución
Si escribimos hanoi(N, origen, auxiliar, destino) para denotar la operación: "pasar N discos del sitio origen al sitio destino usando el sitio auxiliar", entonces podemos escribir el problema como hanoi(N, A, B, C)
La regla 2 nos indica que, para poder pasar el disco más grande (N) hacia el destino C, primero debemos lograr ubicar los primeros N-1 discos en el sitio auxiliar B. Una vez que lleguemos a este estado podemos pasar en un sólo movimiento el disco N desde A hacia C y sólo nos resta desplazar los N-1 discos desde B hacia C para completar nuestro objetivo.
Como se ve, ésta es una estrategia recursiva, que puede escribirse como sigue:
Se puede avanzar un poco más en el pseudocódigo y definir una función que retorne la secuencia de movimientos necesarios para resolver el problema. Para esto, se utiliza una lista de movimientos.
Un movimiento esta definido a partir de un par de sitios que exponen desde y hacia donde se debe mover un disco. Se puede denotar de la siguiente manera:
Movimiento : (A,B)
Esto implica que el disco que esté más arriba de A debe ser movido hacia B. La estructura de la solución es similar a la planteada anteriormente:
hanoi : CARDINAL* Sitio * Sitio * Sitio → ListaMovimientos
La función recibe la cantidad (el número CARDINAL) de discos a mover y los nombres de los sitios a utilizar para hacer los movimientos. El primer sitio implica desde donde parten los N discos y el último el destino de estos. El sitio del centro (2º parámetro) es utilizado como un lugar temporal donde colocar los discos cuando sea necesario.
El caso base es:
hanoi (1, A, TMP, B) = (A,B).[]
Cuando se tiene un solo disco, se debe retornar la lista con el elemento que muestra la manera en que ese disco debe ser movido. El caso recursivo queda de la siguiente manera:
hanoi (N, A, TMP, B) = append1 (append (hanoi (N-1, A, B, TMP), hanoi(1, A, TMP, B)), hanoi(N-1, TMP, A, B))
En caso de tener más de un disco se concatena la información necesaria para mover N-1 discos desde A hacia TMP con el movimiento (A,B). Luego se le agrega al final de esta lista, una nueva que contenga la información de cómo se mueven N-1 discos desde TMP hacia B.
hanoi (N, A, TMP, B) = append(append (hanoi (N - 1, A, B, TMP), hanoi(1, A, TMP, B)), hanoi(N - 1, TMP, A, B))
En caso de tener más de un disco se concatena la información necesaria para mover N-1 discos desde A hacia TMP con el movimiento (A,B). Luego se le agrega al final de esta lista, una nueva que contenga la información de cómo se mueven N-1 discos desde TMP hacia B.
Cantidad de movimientos
El número de movimientos total requerido puede formularse a partir de la estructura del algoritmo:
h(N) = h(N - 1) + 1 + h(N - 1) cuya forma cerrada es h(N) = 2^N – 1.
-------------------------------------------------------------------------------------
Ejercicio 15:
Introducción
La idea de este ejercicio es saber cuántos elementos son necesarios (tomados del final de la lista) para que sumen al menos una cantidad c.
Ejemplo
Si tenemos la lista 1,3,5,4 y queremos sumar al menos 10, debemos tomar los últimos 3 elementos (3, 5 y 4) que suman 12. Los últimos dos no bastan pues suman 9.
Idea de la solución planteada
Muy informalmente, la idea general de la solución es realizar operaciones a la “ida” de la recursión, y luego realizar otras operaciones a la “vuelta” de la recursión. Por “ida” se entiende a las acciones efectuadas antes de las llamadas recursivas, y por “vuelta” las acciones efectuadas después de las llamadas recursivas.
En nuestro caso, a la “ida” no vamos a realizar ninguna acción, sino que simplemente realizaremos la invocación recursiva para desarmar la lista, en donde cada elemento x de la lista haya quedado en el alcance de una invocación. A la “vuelta” recién vamos a procesar la lista, fijándonos cuánto nos falta para llegar a c, y cuántos elementos vamos utilizando. En el paso base será necesario establecer los valores iniciales (falta todo por sumar y aún no utilicé ningún elemento).
Debido a que utilizaremos esta forma de resolución, que implica saber en cada paso de la “vuelta” cuántos elementos utilizamos y cuánto nos falta por sumar, es que no podemos resolver el problema solamente en términos de la propia función SumaC, ya que ésta solo nos devuelve un Natural, y nosotros queremos que nos devuelva dos Naturales (el a que representará cuánto falta, y el b que representará cuántos elementos vamos utilizando). Por esto es que necesitamos una función auxiliar (Suma, que sea recursiva) que nos devuelva esos dos valores en forma de dupla, ya que de esa manera estamos devolviendo un solo valor compuesto de otros dos (una pareja).
Solución planteada:
La solución se presenta a continuación. Se recomienda fuertemente intentar entender la solución, y luego, si no se entiende, leer los comentarios en la siguiente sección.
Comentarios:
A continuación se describe de forma pormenorizada la función auxiliar Suma. Primero se desarma toda la lista, hasta llegar al caso base (lista vacía), donde se devuelve el par (c, 0) indicando que aún no se utilizó ningún elemento y que todavía falta una cantidad c para terminar (es decir que falta todo, porque recién ahora que las llamadas recursivas terminaron, vamos a empezar a hacer algo).
Luego que se desarmó toda la lista gracias a todas las llamadas recursivas, y que para el caso base devolvimos (c, 0), empieza la “vuelta de la recursión”, es decir que todas las llamadas recursivas que se hicieron durante el desarme de la lista, ahora deben completarse y efectivamente devolver un resultado (una pareja). Recordar que hasta ahora se hicieron muchas llamadas recursivas pero se devolvió un resultado (c, 0).
La idea general es que, a partir del primer resultado devuelto por la última invocación (c, 0) empezamos a analizar los elementos de la lista de atrás hacia delante, del último al primero.
Ya que la primer llamada recursiva que se completará será la última (la que desarmó al último elemento), en ella tenemos a disposición el último elemento de la lista. En la penúltima llamada recursiva, tendremos el resultado devuelto por la última llamada más el penúltimo elemento de la lista. En la antepenúltima llamada recursiva, tendremos el resultado devuelto por la penúltima llamada recursiva más el antepenúltimo elemento, etc.
Por lo tanto, “a la vuelta de la recursión” analizaremos los elementos de la lista de atrás hacia delante, con esto lograremos sumar desde atrás hasta obtener al menos una cantidad c. Para esto, en cada paso de la “vuelta”, lo primero que hacemos es fijarnos cuánto falta para terminar, es decir ver el valor de a. Si no falta nada para terminar (a=0), es porque ya sumamos una cantidad mayor o igual que c, entonces devolvemos (0, b). Es muy importante ver que aunque ya llegamos al resultado pedido, tenemos que completar la vuelta de la recursión hacia atrás. No podemos simplemente cortar la ejecución.
Si todavía falta por terminar (a>0), obviamente vamos a considerar el elemento actual (x), por eso vamos a devolver en la segunda componente b+1, porque estamos considerando al elemento actual x para la suma y nos faltará por considerar a-x (se devuelve en la primera componente), ya que nos quedaba a de la recursión anterior y usamos el x actual.
¿Pero qué sucede si el x actual resulta ser más grande que el a? Por ejemplo, nos falta sumar 5 y nos encontremos con un 9. En este caso, se fuerza el resto en cero (a:=0), devolviendo (0, b+1). Y como devolvemos (0, b+1), de ahora en más todas las recursiones siguientes van a ver el cero y van a seguir devolviendo (0, b+1), hasta llegar al final. Notar que hay que devolver b+1 porque aunque el x actual alcanzaba y sobraba, igual lo utilizamos, por lo tanto pasamos de b a b+1.
Solución Alternativa
Esta solución presenta una alternativa a la función Suma. Básicamente, en lugar de considerar a los parámetros de retorno como cuanto falta para llegar a “c” y cuantos elementos se utilizaron; se consideran como la cantidad de elementos sumados y el resultado de la suma. De esta forma se logra el mismo efecto reduciendo los casos a considerar en el paso recursivo.
No pondré los códigos en Modula acerca de las soluciones seleccionadas, sino que les daré un pseudocódigo a modo explicativo de cómo debería funcionar la solución, de este modo ustedes tendrán más o menos un camino a seguir y volver a intentar. Esto contribuirá a que tengan que pensar mucho para lograr aplicar la recursividad y así logren comprenderla de verdad. Obviamente yo estaré disponible para cualquier consulta que tengan ya que algunos ejercicios son muy complicados.
====================================================================================
Ejercicio 1:
Si ambas listas son vacías las listas son iguales y se devuelve true.
Si cualquiera de las listas es vacía, las listas son distintas y se devuelve false, de lo contrario, se obtiene el primer elemento de cada lista y se comparan. Si ambos elementos son iguales se llama recursivamente a la función con el resto de cada una de las listas.
Si los elementos del comienzo de cada una de las listas son diferentes, las listas también son distintas (en por lo menos un elemento), por lo que se devuelve false y las llamadas recursivas terminan.
-------------------------------------------------------------------------------------
Ejercicio 10:
La primera dificultad del ejercicio consiste en decidir sobre qué tipo inductivo se va a definir la función. Resulta claro que el resultado de la función es un natural. Por lo tanto tendríamos:
CaminosPosibles → Retorna un CARDINAL.
Además podría pensarse que la función es sobre una lista (vinculada a los adoquines) y un número natural (que indica el adoquín objetivo). Esto nos daría:
CaminosPosibles: LNat → CARDINAL
Esta notación indica que la función recibe algo de tipo LNat y retorna algo del tipo CARDINAL, tal como la notación matemática para funciones. Es decir
NombreDeLaFunción: Dominio (es decir lo que recibe) → Codominio (es decir, lo que retorna).
De todas formas tratemos de resolver el problema con menos información , esto es, solo con el natural que indique el adoquín objetivo. Entonces definimos nuestra función así:
CaminosPosibles: CARDINAL → CARDINAL
es decir, recibe un CARDINAL y devuelve un CARDINAL.
Exploremos si con esta definición se puede realizar lo pedido. Además como primera aproximación hagamos una tabla que tenga el largo de la lista y la cantidad de caminos posibles. La cantidad de caminos posibles se halla mediante una búsqueda exhaustiva.

Teniendo en cuenta las condiciones:
- De un adoquín numerado i se puede saltar al adoquín numerado i+1.
- De un adoquín numerado i se puede saltar al adoquín numerado i+2 (sin pasar por el adoquín i+1).

Supongamos que queremos calcular la cantidad de caminos para N = 4. En la Figura se ven los caminos posibles para N = 3 y para N = 2, luego por la condición 1 se hace un salto de un adoquín para obtener algunos de los caminos para N = 4, partiendo de los caminos de N = 3. El resto de los caminos se obtienen tomando los caminos para N = 2 y aplicando la condición 2, saltando 2 adoquines. Como estos son todos los caminos posibles, podemos pasar a formalizar:
- Código:
cantidadCaminos: Nat -> Nat
cantidadCaminos(N) = si N = 1 => 1, si N = 2 => 2
si N>= 3 => cantidadCaminos(N-1) + cantidadCaminos(N-2)
Ejercicio 12: Problema de las Torres de Hanoi
El problema de las Torres de Hanoi es un puzzle matemático o juego inventado en 1831. Dicho juego consta de N discos, todos de tamaños diferentes, y 3 sitios, A, B y C (también llamados cilindros) en donde se pueden apilar los discos. En el estado inicial los N discos se encuentran apilados de menor a mayor en el cilindro A, formando una torre tal como se indica en la Figura 1.

En el estado final los N discos se encuentran apilados de menor a mayor en el cilindro C, formando una torre tal como se indica en la Figura 2.

Para alcanzar este objetivo debemos tener en cuenta dos reglas:
- Un disco NO puede colocarse encima de otro más chico que él.
- Sólo puede pasarse un disco a la vez.
Una solución
Si escribimos hanoi(N, origen, auxiliar, destino) para denotar la operación: "pasar N discos del sitio origen al sitio destino usando el sitio auxiliar", entonces podemos escribir el problema como hanoi(N, A, B, C)
La regla 2 nos indica que, para poder pasar el disco más grande (N) hacia el destino C, primero debemos lograr ubicar los primeros N-1 discos en el sitio auxiliar B. Una vez que lleguemos a este estado podemos pasar en un sólo movimiento el disco N desde A hacia C y sólo nos resta desplazar los N-1 discos desde B hacia C para completar nuestro objetivo.
Como se ve, ésta es una estrategia recursiva, que puede escribirse como sigue:
- Código:
hanoi( N, origen, auxiliar, destino){
si (N > 0) entonces
hanoi(N - 1, origen, destino, auxiliar)
imprimir (“pasar disco ”, N, “ de ”, origen, “ a”, destino)
hanoi(N - 1, auxiliar, origen, destino)
fin-si
}
Se puede avanzar un poco más en el pseudocódigo y definir una función que retorne la secuencia de movimientos necesarios para resolver el problema. Para esto, se utiliza una lista de movimientos.
Un movimiento esta definido a partir de un par de sitios que exponen desde y hacia donde se debe mover un disco. Se puede denotar de la siguiente manera:
Movimiento : (A,B)
Esto implica que el disco que esté más arriba de A debe ser movido hacia B. La estructura de la solución es similar a la planteada anteriormente:
hanoi : CARDINAL* Sitio * Sitio * Sitio → ListaMovimientos
La función recibe la cantidad (el número CARDINAL) de discos a mover y los nombres de los sitios a utilizar para hacer los movimientos. El primer sitio implica desde donde parten los N discos y el último el destino de estos. El sitio del centro (2º parámetro) es utilizado como un lugar temporal donde colocar los discos cuando sea necesario.
El caso base es:
hanoi (1, A, TMP, B) = (A,B).[]
Cuando se tiene un solo disco, se debe retornar la lista con el elemento que muestra la manera en que ese disco debe ser movido. El caso recursivo queda de la siguiente manera:
hanoi (N, A, TMP, B) = append1 (append (hanoi (N-1, A, B, TMP), hanoi(1, A, TMP, B)), hanoi(N-1, TMP, A, B))
En caso de tener más de un disco se concatena la información necesaria para mover N-1 discos desde A hacia TMP con el movimiento (A,B). Luego se le agrega al final de esta lista, una nueva que contenga la información de cómo se mueven N-1 discos desde TMP hacia B.
hanoi (N, A, TMP, B) = append(append (hanoi (N - 1, A, B, TMP), hanoi(1, A, TMP, B)), hanoi(N - 1, TMP, A, B))
En caso de tener más de un disco se concatena la información necesaria para mover N-1 discos desde A hacia TMP con el movimiento (A,B). Luego se le agrega al final de esta lista, una nueva que contenga la información de cómo se mueven N-1 discos desde TMP hacia B.
Cantidad de movimientos
El número de movimientos total requerido puede formularse a partir de la estructura del algoritmo:
h(N) = h(N - 1) + 1 + h(N - 1) cuya forma cerrada es h(N) = 2^N – 1.
-------------------------------------------------------------------------------------
Ejercicio 15:
Introducción
La idea de este ejercicio es saber cuántos elementos son necesarios (tomados del final de la lista) para que sumen al menos una cantidad c.
Ejemplo
Si tenemos la lista 1,3,5,4 y queremos sumar al menos 10, debemos tomar los últimos 3 elementos (3, 5 y 4) que suman 12. Los últimos dos no bastan pues suman 9.
Idea de la solución planteada
Muy informalmente, la idea general de la solución es realizar operaciones a la “ida” de la recursión, y luego realizar otras operaciones a la “vuelta” de la recursión. Por “ida” se entiende a las acciones efectuadas antes de las llamadas recursivas, y por “vuelta” las acciones efectuadas después de las llamadas recursivas.
En nuestro caso, a la “ida” no vamos a realizar ninguna acción, sino que simplemente realizaremos la invocación recursiva para desarmar la lista, en donde cada elemento x de la lista haya quedado en el alcance de una invocación. A la “vuelta” recién vamos a procesar la lista, fijándonos cuánto nos falta para llegar a c, y cuántos elementos vamos utilizando. En el paso base será necesario establecer los valores iniciales (falta todo por sumar y aún no utilicé ningún elemento).
Debido a que utilizaremos esta forma de resolución, que implica saber en cada paso de la “vuelta” cuántos elementos utilizamos y cuánto nos falta por sumar, es que no podemos resolver el problema solamente en términos de la propia función SumaC, ya que ésta solo nos devuelve un Natural, y nosotros queremos que nos devuelva dos Naturales (el a que representará cuánto falta, y el b que representará cuántos elementos vamos utilizando). Por esto es que necesitamos una función auxiliar (Suma, que sea recursiva) que nos devuelva esos dos valores en forma de dupla, ya que de esa manera estamos devolviendo un solo valor compuesto de otros dos (una pareja).
Solución planteada:
La solución se presenta a continuación. Se recomienda fuertemente intentar entender la solución, y luego, si no se entiende, leer los comentarios en la siguiente sección.
- Código:
SumaC : LNat*Cardinal → Cardinal , es decir, recibe una lista y un número cardinal, devolviendo otro Cardinal.
SumaC (LNat, c) = b siendo (a, b) = Suma (LNat, c)
- Código:
Suma : LNat * Cardinal → Cardinal*Cardinal , es decir, retorna dos Cardinal.
Suma (LNat vacía, c) = (c, 0)
Suma (LNat no vacía, c) = if (a=0) then (0, b)
else if (x<=a) then (a-x, b+1)
else (0, b+1)
siendo (a, b) = Suma (LNat, c)
Comentarios:
A continuación se describe de forma pormenorizada la función auxiliar Suma. Primero se desarma toda la lista, hasta llegar al caso base (lista vacía), donde se devuelve el par (c, 0) indicando que aún no se utilizó ningún elemento y que todavía falta una cantidad c para terminar (es decir que falta todo, porque recién ahora que las llamadas recursivas terminaron, vamos a empezar a hacer algo).
Luego que se desarmó toda la lista gracias a todas las llamadas recursivas, y que para el caso base devolvimos (c, 0), empieza la “vuelta de la recursión”, es decir que todas las llamadas recursivas que se hicieron durante el desarme de la lista, ahora deben completarse y efectivamente devolver un resultado (una pareja). Recordar que hasta ahora se hicieron muchas llamadas recursivas pero se devolvió un resultado (c, 0).
La idea general es que, a partir del primer resultado devuelto por la última invocación (c, 0) empezamos a analizar los elementos de la lista de atrás hacia delante, del último al primero.
Ya que la primer llamada recursiva que se completará será la última (la que desarmó al último elemento), en ella tenemos a disposición el último elemento de la lista. En la penúltima llamada recursiva, tendremos el resultado devuelto por la última llamada más el penúltimo elemento de la lista. En la antepenúltima llamada recursiva, tendremos el resultado devuelto por la penúltima llamada recursiva más el antepenúltimo elemento, etc.
Por lo tanto, “a la vuelta de la recursión” analizaremos los elementos de la lista de atrás hacia delante, con esto lograremos sumar desde atrás hasta obtener al menos una cantidad c. Para esto, en cada paso de la “vuelta”, lo primero que hacemos es fijarnos cuánto falta para terminar, es decir ver el valor de a. Si no falta nada para terminar (a=0), es porque ya sumamos una cantidad mayor o igual que c, entonces devolvemos (0, b). Es muy importante ver que aunque ya llegamos al resultado pedido, tenemos que completar la vuelta de la recursión hacia atrás. No podemos simplemente cortar la ejecución.
Si todavía falta por terminar (a>0), obviamente vamos a considerar el elemento actual (x), por eso vamos a devolver en la segunda componente b+1, porque estamos considerando al elemento actual x para la suma y nos faltará por considerar a-x (se devuelve en la primera componente), ya que nos quedaba a de la recursión anterior y usamos el x actual.
¿Pero qué sucede si el x actual resulta ser más grande que el a? Por ejemplo, nos falta sumar 5 y nos encontremos con un 9. En este caso, se fuerza el resto en cero (a:=0), devolviendo (0, b+1). Y como devolvemos (0, b+1), de ahora en más todas las recursiones siguientes van a ver el cero y van a seguir devolviendo (0, b+1), hasta llegar al final. Notar que hay que devolver b+1 porque aunque el x actual alcanzaba y sobraba, igual lo utilizamos, por lo tanto pasamos de b a b+1.
Solución Alternativa
Esta solución presenta una alternativa a la función Suma. Básicamente, en lugar de considerar a los parámetros de retorno como cuanto falta para llegar a “c” y cuantos elementos se utilizaron; se consideran como la cantidad de elementos sumados y el resultado de la suma. De esta forma se logra el mismo efecto reduciendo los casos a considerar en el paso recursivo.
- Código:
SumaC : LNat * Cardinal → Cardinal
SumaC (LNat, c) = b siendo (a, b) = Suma (Xs, c)
- Código:
Suma : LNat * Cardinal → Nat * Nat
Suma (LNat vacía, c) = (0, 0)
Suma (LNat no vacía, c) = if (a >= c) then (a, b)
else (a+x, b+1)
siendo (a, b) = Suma (LNat, c)
 Temas similares
Temas similares» Soluciones lección 005
» Soluciones lección 038
» Soluciones lección 006
» Soluciones lección 032
» Soluciones lección 009
» Soluciones lección 038
» Soluciones lección 006
» Soluciones lección 032
» Soluciones lección 009
Página 1 de 1.
Permisos de este foro:
No puedes responder a temas en este foro.


